Honey-Comb
Honey-Comb
Everybody knows that the cells of the honey-comb are 6-sided, and I presume most people know why they are 6-sided. If they were square, the young bee would have a much more uncomfortable cradle in which to grow up, and it would take a much greater space to accommodate a given number of bees. This last would, of itself, be a fatal objection; for to have the greatest benefit of the accumulated animal heat of the brood, they must be closely packed together. This is not only the case with the unhatched bees, but with the bees of a whole colony in winter; when each bee is snugly ensconced in a cell, they occupy less room than they could by any other arrangement.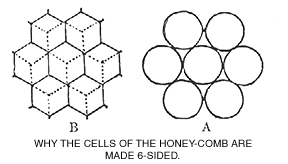
If the cells were round, they could be grouped together much in the same way as they are now; viz., one in the center, and 6 all around it, equally distant from the central one, and from each other, like the cut, in the figure A; but even then, the circles will leave much waste room in the corners, that the bees would have to fill with wax.
At B, we see the cells are nearly as comfortable for the young bee as a round one would be of course. I mean from our point of view, for it is quite likely that the bees know just what they need a great deal better than we do and, at the same time, they come together in such a way that no space is left to be filled up at all. The bees, therefore, can make the walls of their cells so thin that they are little more than a silky covering, as it were, that separates each one from it’s neighbor. It must also be remembered that a bee, when in his cell, is squeezed up, if we may so term it, so as to occupy much less space than he otherwise would; and this is why the combined animal heat of the cluster is so much better economized in winter, when the bees have a small circle of empty cells to cluster in, with sealed stores all around them.
But, my friends, this is not half of the ingenuity displayed about the cell of the bee. These hexagonal cells must have some kind of a wall or partition between the inmates of one series of cells, and those in the cells on the opposite side. If we had a plain partition running across the cell at right angles with the sides, the cells would have flat bottoms which would not fit the rounded body of the bee, besides leaving useless corners, just as there would have been if the cells had been made round or square. Well, this problem was solved in much the same way, by making the bottom of the cell of three little lozenge-shaped plates. In the figure below we give one of these little plates, and also show the manner in which three of them are put together to form the bottom of the cell.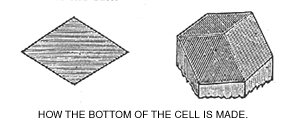
If the cells were round, they could be grouped together much in the same way as they are now; viz., one in the center, and 6 all around it, equally distant from the central one, and from each other, like the cut, in the figure A; but even then, the circles will leave much waste room in the corners, that the bees would have to fill with wax.
Now, if the little lozenge plates were square, we should have much the same arrangement, but the bottom would be too sharp-pointed, as it were, to use wax with the best economy, or to best accommodate the body of the infantile bee. 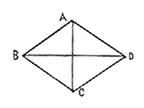 Should we, on the contrary, make the lozenge a little longer, we should have the bottom of the cell too nearly flat, to use wax with most economy, or for the comfort of the young bee. Either extreme is bad, and there is an exact point, or rather a precise proportion that the width of this lozenge should bear to the length. This proportion has been long ago decided to be such that, if the width of the lozenge is equal to the side of a square, the length should be exactly equal to the diagonal of this same square. This has been proven by quite an intricate geometrical problem; but a short time ago, while getting out our machine for making the foundation, I discovered a much shorter way of working this beautiful problem.
Should we, on the contrary, make the lozenge a little longer, we should have the bottom of the cell too nearly flat, to use wax with most economy, or for the comfort of the young bee. Either extreme is bad, and there is an exact point, or rather a precise proportion that the width of this lozenge should bear to the length. This proportion has been long ago decided to be such that, if the width of the lozenge is equal to the side of a square, the length should be exactly equal to the diagonal of this same square. This has been proven by quite an intricate geometrical problem; but a short time ago, while getting out our machine for making the foundation, I discovered a much shorter way of working this beautiful problem.
In the figure above, let A B C D represent the lozenge at the bottom of the cell, and A C, the width, while B D is the length of said lozenge. Now, the point I wish to prove is, that A C bears the same proportion to B D that the side of a square does to the diagonal of the same square.
THE MATHEMATICS OF THE HONEY-COMB.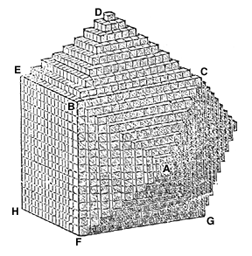
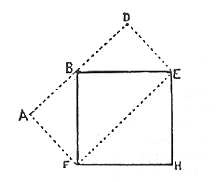
Suppose we have a cubical block, E B C G F, and that we pile small blocks on its sides as shown, so as to raise pyramids of such an inclination that a line from any apex to the next, as from A to D, will just touch the edge of the cube, B C. Now A C D B is the geometric lozenge we are seeking. Its width, B C, is equal to one side of the square, E B F H, for it is one side of the cube. Now, to prove that A D is equal to the diagonal E F, we will use the diagram below.
Let E B F H represent the cube, and the dotted lines the pyramids. If the pyramids are so made that the line A D is a straight, continuous one, it is evident, by a little reflection, that the angles A and D will be right angles. If this is so, A D is exactly equal to E F, the point we were to prove. Now, referring to the former figure, if we should go on building these pyramids on all sides of the cube, we will have the beautiful geometrical figure called the rhombic dodecahedron; it is so called, because it is a solid figure having 12 equal sides, and each side is a rhomb, or lozenge, such as we have described. Where the obtuse angles of three of these rhombs meet, as at C, we shall have the exact figure of the bottom of a honey-comb cell. A picture of the geometrical solid we have mentioned is given below.
 How does it come that the bees have solved so exactly this intricate problem, and know in just what form and shape their precious wax can be used, so as to hold the most honey, with the very least expenditure of labor and material? Some are content with saying that they do it by instinct, and let it drop there; but I believe God has given us something farther to do than to invent names for things, and then let them drop. By carefully studying the different hives in a large apiary, we see that not all of them build comb precisely alike, and not all colonies are equally skilled in working wax down to this wonderful thinness. Some bees will waste their precious moment and wax in making great, awkward lumps of wax; coarse, irregular cells; crooked, uneven comb, etc., with very bad economy either for the production of brood or for the storing of honey; while others will have all their work so even and true, and so little wax will be wasted, that it is wonderful to contemplate the regularity and system with which the little fellows have labored. Now, it does not require any great amount of wisdom to predict that the latter would, in a state of nature, stand a far better chance of wintering than the ones that were wasteful and irregular in their ways of doing things. If this be the case, those queens whose progeny were best laborers, most skillful wax-workers, as well as most energetic honey-gatherers, would be most sure to perpetuate themselves, while the others would, sooner or later, become extinct. I have found more of a tendency in bees to sport, or to show queer peculiarities, than in any other department of the animal or vegetable kingdom. They vary in color, in shape, in size, in disposition, in energy; and almost every colony, if studied closely, will be found to have some little fashion or way of doing things, different from all the rest in the apiary. Now, when we take into account the fact that many generations can be reared in a single summer, we see how rapidly, by fostering and encouraging any desirable trait or disposition, the bees may be molded to our will. The egg that is laid by a queen to-day may, by proper care, be made to produce a queen laying eggs of the same kind herself, in the short time of only 25 days, as I have explained heretofore. Well, if we should pick out a queen whose progeny made the thinnest comb, and rear others from her, doing the same thing for several generations, we should probably get bees whose combs would break down by the weight of the honey. In a state of nature this extreme would correct itself, as well as the other; but the point I wish you to see is right here: Geometrical accuracy in the shape of the cells can never be overdone, and can be reached only by absolute perfection; and this absolute perfection, the bees have been constantly aiming at through endless ages. Is it any thing strange, my friends, that the bees have got the honey-comb pretty nearly right by this time? I will give you a little story, and one which has been very interesting to me, from page 150, Vol. II., American Bee Journal.
How does it come that the bees have solved so exactly this intricate problem, and know in just what form and shape their precious wax can be used, so as to hold the most honey, with the very least expenditure of labor and material? Some are content with saying that they do it by instinct, and let it drop there; but I believe God has given us something farther to do than to invent names for things, and then let them drop. By carefully studying the different hives in a large apiary, we see that not all of them build comb precisely alike, and not all colonies are equally skilled in working wax down to this wonderful thinness. Some bees will waste their precious moment and wax in making great, awkward lumps of wax; coarse, irregular cells; crooked, uneven comb, etc., with very bad economy either for the production of brood or for the storing of honey; while others will have all their work so even and true, and so little wax will be wasted, that it is wonderful to contemplate the regularity and system with which the little fellows have labored. Now, it does not require any great amount of wisdom to predict that the latter would, in a state of nature, stand a far better chance of wintering than the ones that were wasteful and irregular in their ways of doing things. If this be the case, those queens whose progeny were best laborers, most skillful wax-workers, as well as most energetic honey-gatherers, would be most sure to perpetuate themselves, while the others would, sooner or later, become extinct. I have found more of a tendency in bees to sport, or to show queer peculiarities, than in any other department of the animal or vegetable kingdom. They vary in color, in shape, in size, in disposition, in energy; and almost every colony, if studied closely, will be found to have some little fashion or way of doing things, different from all the rest in the apiary. Now, when we take into account the fact that many generations can be reared in a single summer, we see how rapidly, by fostering and encouraging any desirable trait or disposition, the bees may be molded to our will. The egg that is laid by a queen to-day may, by proper care, be made to produce a queen laying eggs of the same kind herself, in the short time of only 25 days, as I have explained heretofore. Well, if we should pick out a queen whose progeny made the thinnest comb, and rear others from her, doing the same thing for several generations, we should probably get bees whose combs would break down by the weight of the honey. In a state of nature this extreme would correct itself, as well as the other; but the point I wish you to see is right here: Geometrical accuracy in the shape of the cells can never be overdone, and can be reached only by absolute perfection; and this absolute perfection, the bees have been constantly aiming at through endless ages. Is it any thing strange, my friends, that the bees have got the honey-comb pretty nearly right by this time? I will give you a little story, and one which has been very interesting to me, from page 150, Vol. II., American Bee Journal.
If a single cell be isolated, it will be seen that the sides rise from the outer edges of the three lozenges above mentioned, so that there are, of course, six sides, the transverse section of which gives a perfect hexagon. Many years ago, Maraldi, being struck with the fact that the lozenge-shaped plates always had the same angles, took the trouble to measure them, and found that in each lozenge the large angles measured 109 degrees 28′, and the smaller 70 degrees 32′, the two together making 180 degrees, the equivalent of two right angles. He also noted the fact that the apex of the three-sided cup was formed by the union of three of the greater angles. The three united lozenges are seen in the figure below.
Some time afterward, Reaumur, thinking that this remarkable uniformity of angle might have some connection with the wonderful economy of space which is observed in the bee-comb, hit upon a very ingenious plan. Without mentioning his reasons for the question, he asked Koenig, the mathematician, to make the following calculation: Given a hexagonal vessel terminated by three lozenge-shaped plates, what are the angles which would give the greatest amount of space with the amount of material?
Koenig made his calculations, and found that the angles were 109 degrees 26′ and 70 degrees 34′, almost precisely agreeing with the measurements of Maraldi. The reader is requested to remember these angles.
Reaumur, on receiving the answer, concluded that the bee had very nearly solved the difficult mathematical problem, the difference between the measurement and the calculation being so small as to be practically negative in the actual construction of so small an object as the bee-cell.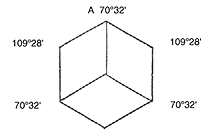
Mathematicians were naturally delighted with the results of the investigation, for it showed how beautifully practical science could be aided by theoretical knowledge; and the construction of the bee-cell became a famous problem in the economy of nature. In comparison with the honey which the cell is intended to contain, the wax is a rare and costly substance, secreted in very small quantities, and requiring much time and a large expenditure of honey for its production. It is, therefore, essential that the quantity of wax employed in making the comb should be as little, and that of the honey which could be stored in it as great, as possible.
For a long time these statements remained uncontroverted. Any one with the proper instruments could measure the angles for himself, and the calculations of a mathematician like Koenig would hardly be questioned. However, Maclaurin, the well-known Scotch mathematician, was not satisfied. The two results very nearly tallied with each other, but not quite, and he felt that, in a mathematical question, precision was a necessity. So he tried the whole question himself, and found Maraldi’s measurement correct namely, 109 degrees 28′, and 70 degrees 32′.
He then set to work at the problem which was worked out by Koenig, and found that the true theoretical angles were 109 degrees 28′ and 70 degrees 32′, precisely corresponding with the actual measurement of the bee-cell.
Another question now arose. How did this discrepancy occur? On investigation, it was found that no blame attached to Koenig, but that the error lay in the book of Logarithms which he used. Thus a mistake in a mathematical work was accidentally discovered by measuring the angles of a bee-cell a mistake sufficiently great to have caused the loss of a ship whose captain happened to use a copy of the same Logarithmic tables for calculating his longitudes.
DIFFERENT KINDS OF CELLS IN THE HONEY-COMB.
The bees build two distinct, regular sizes drone and worker cells. The worker-comb measures very nearly five cells to the inch, on an average. Some specimens average a little larger, and some a little smaller; but when the comb is at all irregular, it is quite apt to be a little larger. The best specimens of true worker-comb generally contain 5 cells within the space of an inch, and therefore this measure has been adopted for the comb foundation. If there are five cells to the inch, a square inch would give, on an average, about 25* cells, and 25 on the opposite side would make 50 young bees that would be hatched from every square inch of solid brood. As foundation is so much more regular than the natural comb, we get a great many more bees in a given surface of comb, and here, at least, we can fairly claim to have improved on nature.
The drone-comb measures just about 4 cells to the inch, but the bees seem less particular about the size of it than with the worker. They very often seem to make the cells of such size as to best fill out a given space; and we, accordingly, find them of all sizes, from worker size all the way up to considerably larger than 1/4 of an inch in width. Drones are raised in these extra-large cells without trouble, and honey is also stored in them; but where they are very large, the bees are compelled to turn them up, or the honey would flow out. As the honey is kept in place by capillary attraction, if the cells exceed a certain size, the adhesion of the liquid to the wax walls is insufficient, of itself, to hold the honey in place. Where drones are to be reared in these very large cells, the bees contract the mouth, by a thick rim. As an experiment, I had some plates made for producing small sheets of foundation, having only 3-1/2 cells to the inch. The bees worked on a few of these, with these same thick rims, but they evidently did not like the idea very well, for they tried to make worker-cells of some of it, and it proved so much of a complication for their little heads that they finally abandoned the whole piece of comb, apparently in disgust. Bees sometimes rear worker brood in drone-comb, where compelled to from want of room, and they always do it in the way I have mentioned, by contracting the mouth of the cells, and leaving the young bee a rather large berth in which to grow and develop. Drones are sometimes reared in worker-cells also, but they are so much cramped in growth that they seldom look like a fully developed insect.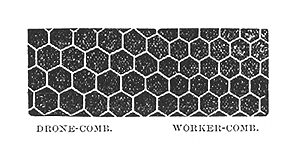
Several times it has been suggested that we enlarge the race of honey-bees by giving them larger cells; and some circumstances seem to indicate that something may be done in this direction, although I have little hope of any permanent enlargement in size, unless we combine with it the idea of selecting the largest bees to propagate from, as given a few pages back. By making the cells smaller than ordinarily, we can get small bees with very little trouble; and I have seen a whole nucleus of bees so small as to be really laughable, just because the comb they were hatched from was set at an angle so that one side was concave and the other convex. The small bees came from the concave side. Their light, active movements, as they sported in front of the hive, made them a pretty and amusing sight for those fond of curiosities. Worker-bees reared in drone cells are, if I am correct, sometimes extra large in size; but as to whether we can make them permanently larger by such a course, I am inclined to doubt. The difficulty, at present, seems to be the tendency to rearing a great quantity of useless drones. By having a hive furnished entirely with worker-comb, we can so nearly prevent the production of drones that it is safe enough to call it a complete remedy.
HOW THE BEES BUILD THE COMB.
In this day and age of bees and honey, it would seem that one should be able to tell how the bees build comb, with almost as much ease as they would tell how cows and horses eat grass; but for all that, we lack records of careful and close experiments, such as Darwin made many years ago. In our house-apiary, there are dozens of hives where the bees are building right up close to the glass, at this very minute; and all one has to do, in order to see how itis done, is to take a chair and sit down before them. But the little fellows have such a queer, sleight-of-hand way of doing the work, that I hardly know how they do accomplish it.
In a little work published by Prof. Agassiz, about the year 1867, the renowned naturalist speaks as follows about the way in which bees build honey-comb:
“The bees stand as close as they can together in their hive for economy of space, and each one deposits his wax around him, his own form and size being the mold for the cells, the regularity of which, when completed, excites so much wonder and admiration. The mathematical secret of the bee is to be found in his structure, not in his instinct.”
Notwithstanding the promptness with which the folly of such a statement was at once shown up in the bee-journals, it seems it never came to the eyes of Prof, A., or, at least, he never deemed it worthy of notice; for, in 1873, he gave, substantially, the same thing in a lecture at Cambridge, Mass., and it was praised and published in the Tribune and other papers, and sent broadcast all over our land. I believe all the bee-journals at once protested against giving the people such “twaddle” (if I may be excused for using the term), as science; but for all that, I think the learned professor never recalled his blunder, or even so much as admitted that he had never seen the inside of a bee-hive at all, but only guessed at it, or repeated what he had been told by some one.
About two years afterward, the great scientist, Tyndall, by some means got an inkling of the way in which Agassiz had “put his foot in it,” and, in the Popular Science Monthly, wisely admitted that the bees did not stand in the cells to build their comb, but fixed them in this way: Says he, “The bees place themselves at equal distances apart upon the wax, and sweep and excavate” etc. Now, if Tyndall is teaching us other things in the same way, i. e.., delivering lectures on some subject on which he knows nothing, how much can we depend on any thing he says? Oh why could not he and Agassiz, before attempting to explain the matter to the people, take the time to get a hive of real live bees, as did Darwin, and not be obliged to take any thing at second hand? If they two were afraid of stings, any expert honey-raiser could afford them the facilities for a safe observation, and thus prevent their going into such folly, or falsehood, to call things by their right names, for they pretend to have knowledge where they have none. Take the money and buy a hive of bees, all ye that thirst for knowledge, and take it direct from God’s own works, instead of receiving it second hand.
For particulars in regard to the North Pole, or as to whether the planet Jupiter is habitable, we may be obliged to listen to those who should know better than we do; but in our own industry no such necessity exists, for a swarm of bees is within the reach of all.
When distinguished persons have visited my apiary, I have almost invariably heard them mention the great discovery of Agassiz, in regard to the way in which bees build their comb; and when I explain that it was a great mistake, they usually think that so great a man as Agassiz, and one who always went to the ants and bees with his own eyes, must have been right, and that I had made a mistake somewhere.
I have occupied all this space, my friends, just to give you an illustration of how little real work some of the great scientists and lecturers are in the habit of doing, and of the importance of proving things for yourself, with your own eyes and hands.
If we examine the bees closely during the season of comb-building and honey-gathering, we shall find many of them with the wax scales protruding between the rings that form the body, and these scales are either picked from their bodies, or from the bottom of the hive or honey-boxes in which they are building. If a bee is obliged to carry one of these wax scales but a short distance, he takes it in his mandibles, and looks as business like with it thus as a carpenter with a board on his shoulder. If he has to carry it from the bottom of the honey-box, he takes it in a way that I can not explain any better than to say he slips it under his chin. When thus equipped, you would never know he was encumbered with any thing, unless it chanced to slip out, when he will very dextrously tuck it back with one of his fore feet. The little plate of wax is so warm from being kept under his chin, as to be quite soft when he gets back; and as he takes it out, and gives it a pinch against the comb where the building is going on, one would think he might stop a while, and put it into place; but not he; for off he scampers and twists around so many different ways, you might think he was not one of the working kind at all. Another follows after him sooner or later, and gives the wax a pinch, or a little scraping and burnishing with his polished mandibles, then another, and so on, and the sum total of all these manoeuvres is, that the comb seems almost to grow out of nothing; yet no bee ever makes a cell himself, and no comb-building is ever done by any bee while standing in a cell; neither do the bees ever stand in rows and “excavate,” or any thing of the kind.
The finished comb is the result of the united efforts of the moving, restless mass; and the great mystery is, that any thing so wonderful can ever result at all from such a mixed-up, skipping-about way of working, as they seem to have. When the cells are built out only part way, they are filled with honey or eggs, and the length is increased when they feel disposed, or “get around to it,” perhaps. It may be that they find it easier working with the shallow walls about the cells, for they can take care of the brood much easier, and put in the honey easier too, in all probability; and, as a thick rim is left around the upper edge of the cell, they have the material at hand to lengthen it at any time. This thick rim is also very necessary to give the bees a secure foothold, for the sides of the cells are so thin they would be very apt to break down with even the light weight of a bee. When honey is coming in rapidly, and the bees are crowded for room to store it, their eagerness is so plainly apparent, as they push the work along, that they fairly seem to quiver with excitement; but for all that, they skip about from one cell to another in the same way, no one bee working in the same spot to exceed a minute or two, at the very outside. Very frequently, after one has bent a piece of wax a certain way, the next tips it in the opposite direction, and so on until completion; but after all have given it a twist and a pull, it is found in pretty nearly the right spot. As nearly as I can discover, they moisten the thin ribbons of wax with some sort of fluid or saliva. As the bee always preserves the thick rib or rim of the comb he is working, the looker-on would suppose he was making the walls of a considerable thickness; but if we drive him away, and break this rim, we will find that his mandibles have come so nearly together that the wax between them, beyond the rim, is almost as thin as tissue paper. In building natural comb, of course the bottoms of the cells are thinned in the same way, as the work goes along, before any side walls are made at all; but the manner of thinning the bottoms of the cells in the foundation is quite another thing.
*The exact mathematical calculation make these numbers 29, 29 and 58, respectively, but ordinarily the numbers I have given in the context are more nearly correct.



